Elastic moduli of
single-walled carbon nanotube bundles
|
|
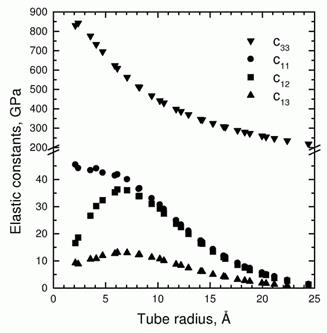
The elastic constants and elastic moduli of an infinite bundle of identical SWNTs forming a 2d triangular lattice are estimated using the long-wavelength limit of the lattice dynamics of the bundle [1]. The intratube interactions are modeled using force constants of the valence force field type. The intertube interactions are described by a Lennard-Jones potential V(r) = 4ε[(σ/r)12–(σ/r)6] transferred from a study of graphite. The energy of bundles of armchair and zigzag tubes with radii 2 Å < R < 25 Å was minimized with respect to the lattice parameter while keeping the tube cross-section circular. In the case of hexagonal symmetry of the bundle, the Young's modulus Y and Poisson ratio v are anisotropic. Let us denote the Young's modulus for directions along and perpendicular to the tube axis by Y|| (longitudinal modulus) and Y^ (transverse modulus), and the corresponding Poisson ratio by v|| and v^ (relative widening of the crystal under lateral forces). The Young's moduli, bulk modulus K and Poisson ratios are related to the elastic constants cij as shown in Table 1. Although the calculations here show that c11, c12, c13 << c33 so that simplified relations can be used (Table 1, last column), here we make use of the exact relations between the elastic constants, on the one hand, and the elastic moduli and Poisson ratio on the other. The calculated c11, c12, c13, and c33 as a function of the tube radius are shown in Fig. 1. The value of a given elastic constant for both armchair and zigzag tubes lies on a smooth curve so that we might expect this to be true for tubes of arbitrary types as well. The constants c12 and c13 reach maximal value for R » 6 Å while c11 has only a kink there. Similar characteristic features can be observed in the radius dependence of some of the moduli and Poisson ratios. Table 1. Relations between the elastic moduli and Poisson ratio, and the elastic constants in the case of hexagonal symmetry. The z-axis is chosen along the tube axis.
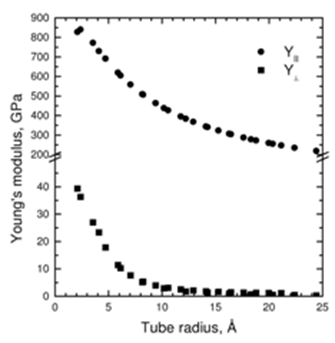
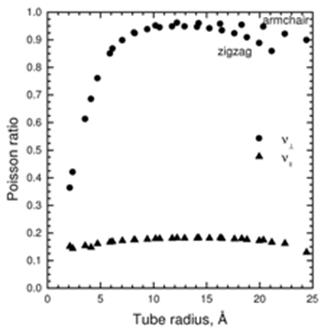
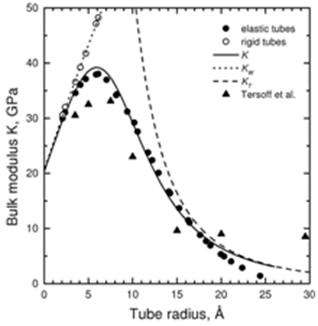
It is evident from Fig. 2 that the inequality Y|| >> Y^ holds for the calculated Young’s moduli and, consequently, high mechanical anisotropy is predicted for the nanotube crystals. The longitudinal modulus Y|| is equal to the elastic constant c33 within less than 1% and decreases inversely proportional to the tube radius for large radii. The transverse modulus Y^ depends mainly on the elastic constants c11 and c12 and is found to decrease more rapidly with R. It is seen in Fig. 3 that the longitudinal Poisson ratio v|| has values that are close to the in-plane one of graphite of 0.17. The calculated Poisson ratio v^ increases steeply with the radius and becomes larger than 0.9 for R > 6 Å. Values of v^ close to unity mean that, under lateral forces, the circular cross section of the tube is deformed to an elliptic one with almost unchanged tube circumference. The change in the behavior of Y^ and v^ near R » 6 Å is due to the competition between the van der Waals interactions and the tube elasticity perpendicular to the tube axis which will be discussed in more detail in the case of the bulk modulus. The calculated bulk modulus K (Fig. 4, solid circles) reaches a maximum at R = 6 Å and decreases to zero at large radii. This behavior of K is a consequence of the interplay of the intertube van der Waals forces (W) and the tube elastic forces (T). In the small-strain limit, these forces can be described by springs with force constants kW and kT, respectively, and the resulting interaction – by a system of these two springs, connected in series, with a force constant k = kWkT/(kW + kT). Then, the bulk modulus K ~ k and therefore K = KWKT/(KW + KT). For small
R, the intertube interaction between rigid tubes gives rise
to For large R, the tube elasticity gives rise to It is seen in Fig. 4 that the calculated K has a maximum value of 38 GPa for R » 6 Å – a result that may be of primary importance for the future industrial application of bulk nanotube materials. It is also clear that the obtained K follows the values of the molecular dynamics study (Tersoff) up to R £ 16 Å. The deviations for R > 16 Å are due to the polygonization of the strained tube, which was allowed in the latter simulations. References 1. V. N. Popov,
V. E. Van Doren, and M. Balkanski,
|
|||||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
||||||||||||||||||||||
|
|
Valentin Popov