Linear elastic properties
of single-walled carbon nanotubes
|
|
The SWNT
can be viewed as an infinite graphene sheet wrapped into a cylinder.
Therefore, one can expect that its axial elasticity will be similar to the
in-plane one of graphene apart from some effects of the tube curvature. The
attempts to estimate the axial elastic moduli of any nanotube immediately
face the difficulty of defining the tube cross-sectional area. Indeed, the
elastic moduli are strictly defined only for homogeneous media when any
choice of the cross-sectional area will give the same result. In the case of
nanotubes, one can assume that a nanotube is a homogeneous cylinder with
inner and outer radii, r and R, respectively. The choice of these radii is quite
ambiguous and so are the derived elastic moduli. There are several ways to
overcome this difficulty by defining the linear stiffness as the axial force
per unit tube perimeter or the axial force per atomic volume. When the moduli,
derived by various techniques, are normalized in any of the two ways, they
are very close to the in-plane ones of graphene. Another
important point is the radius dependence of the elastic moduli. The results
of the various approaches show softening of the moduli at small tube radii.
The usual technique to estimate the moduli is based on the calculation of the
energy of the axially strained tube. Another technique estimates the moduli
from the slope of the LA and TW phonon branches of the phonon dispersion of
the nanotubes calculated using a phenomenological lattice-dynamical model
[1]. Instead of obtaining the slope of the branches numerically, one can use
expressions for the moduli derived in the long-wavelength limit of the
lattice dynamics of the nanotubes [2]. The MWNTs can be treated in the same
way as SWNTs. The
elastic moduli of a number of chiral and achiral SWNTs are calculated within
the long-wavelength limit of the lattice dynamics based on force constants of
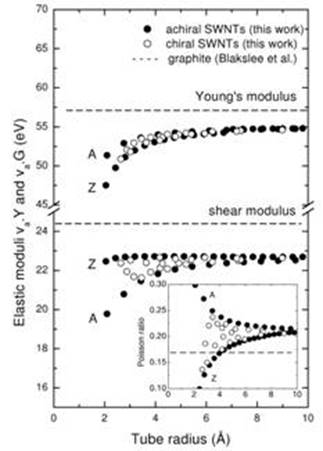
the valence force field type [1,2]. The Young's and shear moduli, Y and G, are normalized on the atomic volume and are given in units of
eV. It is clear from Fig. 1 that for a given radius Y for armchair tubes is slightly larger than for zigzag tubes
while for chiral tubes it has intermediate values. It tends to about 55 eV
for large radii and softens to about 50 eV for small radii. G tends to about 23 eV for large radii
and softens at small radii. Both moduli exhibit slight chirality dependence. Using Y and G, we can estimate the Poisson ratio, v, that is equal to the ratio of the relative radial expansion to
the relative axial tube shortening, making use of the expression valid for
the three-dimensional isotropic medium v
= (Y/2 – G)/G. The spread in the
values of both moduli has as a consequence a spread in the values of Poisson
ratio that is more prominent for small tube radii. In the limit of large
radii, Y, G, and v are equal to
the experimental in-plane ones within several per cent. Fig. 1.
Calculated Young’s and shear moduli times the volume per atom of the tube va
(in eV), and Poisson ratio estimated using the relation ν = (Y/2 – G)/G
(inset) versus tube radius for various chiral and achiral SWNTs [2]. The
letters A and Z stand for “armchair” and “zigzag”, respectively. References 1. V. N. Popov, V. E. Van Doren, and M. Balkanski, Phys. Rev. B 59 (1999)
8355-8358. 2. V. N. Popov, V. E. Van Doren, and M. Balkanski, Phys. Rev. B 61 (2000) 3078-3084. |
Valentin Popov