Electronic band structure, phonon dispersion, breathing-like and shear modes of fewlayer graphene
|
|
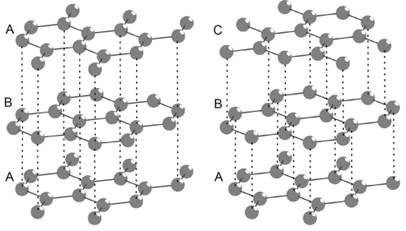
Fewlayer graphene (FLG) consists of several graphene layers, stacked in
various ways. The special cases of stacking are: AA-stacked FLG, which is not
a stable structure, AB-stacked or Bernal FLG, and ABC-stacked or rhombohedral
FLG. Here, we consider only AB- and ABC-stacked FLG (Fig. 1). These
structures have hexagonal symmetry with a hexagonal Brillouin zone.
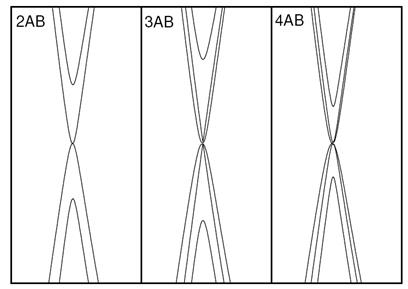
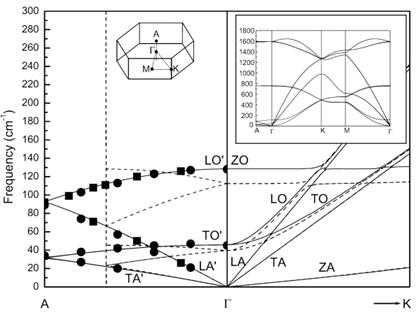
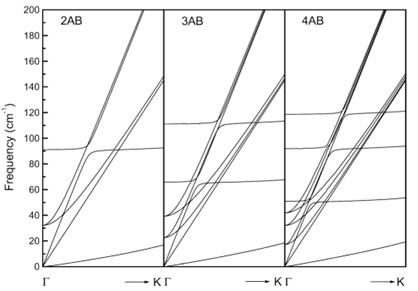
The electronic band structure of FLG is calculated within a non-orthogonal tight-binding (NTB) model with intralayer parameters, taken over from an ab-initio study (Porezag), and interlayer parameters, taken from another ab-initio study [3]. The phonon dispersion of FLG is calculated within the NTB model using a perturbative approach [4,5]. It has to be noted, that the ab-initio derived parameters account only for part of the electron-electron interactions and additional pair potential has to be introduced in order to obtain electronic band structure, which is in agreement with the ab-initio one. In the case of the interlayer interaction, the additional pair potential was derived by fitting to the breathing and shear modes, and to the cohesive energy of the graphene layers of AB-stacked graphite. Figure 2 shows a part of the electronic band structure of AB-stacked FLG in the energy region between −0.75 and +0.75 eV with respect to the Fermi energy, taken as zero, and in the vicinity of the K point of the Brillouin zone. The interlayer interaction lifts the degeneracy of the electronic bands, the splitting in the optical region of −1.5 to +1.5 being as large as 1 eV. Apart from the splitting, the electronic bands change their character in the vicinity of the Fermi energy. Namely, the two linear bands of graphene are modified to four parabolic bands for 2AB, two linear bands and 4 parabolic ones for 3AB, 6 parabolic bands for 4AB, etc. It has to be noted that the relative large splitting of the bands plays important role for transport and optical phenomena. Figure 3 shows the phonon dispersion of AB- and ABC-stacked graphite. The phonon branches of AB-stacked graphite along the ΓA direction are in excellent agreement with the available experimental data. It is clearly seen, that the interlayer interaction produces major modification only of the acoustic branches, while leaving the higher-frequency branches almost unchanged, apart from splitting up to a few cm-1 (Fig. 2, inset). Figure 4 shows the obtained low-frequency phonon dispersion of AB-stacked FLG. Apart from the acoustic branches with longitudinal (L), transverse (T), and out-of-plane (Z) character, denoted as LA, TA, and ZA, the interlayer interaction brings about additional optical phonon branches due to lifting of the N-fold degeneracy of the acoustic branches. In particular, N-layer AB-stacked graphene (or NAB graphene) has 3N – 3 additional optical branches, among which there are N – 1 LO branches, N – 1 TO branches, and N – 1 ZO branches. The ZO phonons have breathing-like displacement of the layers (breathing modes or BM), the LO+TO phonons have shear displacement of the layers (shear modes or SM). We note that the low-frequency phonon dispersion of N-layer ABC-stacked FLG is indistinguishable from that of AB-stacked FLG for the same number of layers (not shown here). The BMs and SMs have frequencies between zero and 126 cm-1, the latter frequency being the BM of AB-stacked graphite. The frequencies of the BMs and SMs can be derived by modeling FLG with any stacking as a linear N-atom molecule, consisting of equally separated identical atoms with nearest-neighbor interactions. It is straightforward to obtain the vibrational frequencies of the molecule as
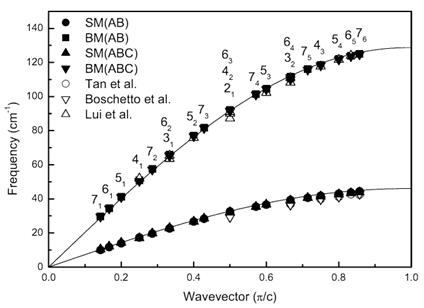
where the index n enumerates the vibrational modes, n = 1, 2 , …, N −1, ω0 is the optical phonon frequency of the infinite atomic chain with two-atom unit cell. The frequencies of the BMs and the SMs can be generated from the expression above by taking ω0 equal to the frequency of the BM and SM of graphite (Fig. 3). Figure 5 shows the graphs of the equation above for the BMs and SMs considering n/N as a continuous dimensionless wavevector in the range from zero to 1. The frequencies of the BMs and SMs, derived from the NTB calculations for AB- and ABC-stacked FLG, are given as solid symbols, while the available experimental data is plotted by empty symbols. It is clearly seen that the NTB frequencies, as well as the predictions of the equation above, are in excellent agreement with the experimental data, which supports the applicability of the used NTB model, as well as the simple mechanical model for the BMs and SMs. References: 1. V. N. Popov, New J. Phys. 6 (2004) 1-17. 2. V. N. Popov and L. Henrard, Phys. Rev. B 70 (2004) 115407. 3. V. N. Popov and Ch. van Alsenoy, Phys. Rev. B 90 (2014) 245429. 4. V. N. Popov, L. Henrard, and Ph. Lambin, Phys. Rev. B 72 (2005) 035436. 5. V. N. Popov and Ph. Lambin, Phys. Rev. B 73 (2006) 085407. |
|
|
|
|
|
|
|
|
|
|
|
Valentin Popov
January 18, 2015