Symmetry-adapted tight-binding model for electronic band structure calculations for single-walled carbon nanotubes (SWNTs)
The electronic band structure problem can be made tractable for all tubes of practical interest (diameters up to 3 nm) if the helical symmetry of the tubes is taken into account [1,2]. It is easier of all to introduce this symmetry in comparison with the translational symmetry of graphene. In graphene, the two-atom unit cell can be mapped unto the entire graphene sheet by use of two primitive translations. Similarly, the two-atom unit cell of the nanotube can be mapped unto the entire tube by means of two different screw operators. A screw operator {S|t} rotates the position vector of an atom at an angle φ about the tube axis and translates it at a vector t along the same axis. Let us label the two-atom unit cells by the vector lattice index by l = (l1,l2), where l1 and l2 are integer numbers, and the atoms in each atomic pair by the integer κ (κ = 1, 2). Then, the equilibrium position vector R(lκ) of the κth atom of the lth unit cell of the tube can be obtained from R(κ) ≡ R(0κ) by means of the two screw operators {S1|t1} and {S2|t2}:
It is convenient to adopt the compact notation 
and
, and to rewrite this equation as
The electronic band structure of SWNTs can be calculated within the independent-electron approximation using the one-electron Schrödinger equation
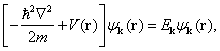
where m is the electronic mass, V(r)
is the effective periodic potential, 
and 
are the one-electron wavefunction and energy depending on the
wavevector k. This equation can be
solved by representing as a linear combination of basis functions 
In the tight-binding approach, the φ's
are constructed from atomic orbitals centered at the atoms. Let us denote by
the rth atomic
orbital centered at the atom with position vector R(l) (the index κ is omitted to avoid confusion
with the wavevector); r = 1, 2, …, 2s, where s =1 for the π-band
tight-binding model and s = 4 for the
all-valence electron tight-binding model. Then, Bloch's condition for the basis
functions is satisfied for the following linear combination of χ's
where Nc is the number of
unit cells in the tube. At this moment, it is convenient to account for the
rotational and translational symmetry of the tubes. Indeed, the one-electron
wavefunction remains unchanged under a rotation of the system at 2π and is a wave along the tube
axis. The two conditions lead to the following restrictions on the quantity k: 
and
, where q is the
one-dimensional wavevector of the tube (
) and l is the
azimuthal quantum number (l = 0, 1,
2, …, N-1). The expression above is
then modified to the form
where 
and 
are the dimensionless coordinates of the unit cell around the
circumference and along the tube axis.
Substituting the φ's in the expression for the ψ's and the latter in the one-electron equation Schrödinger equation, one easily obtains the non-orthogonal tight-binding equations
where the quantities 
and 
are given by
and
Here, 
and 
are the Hamiltonian and overlap matrix elements,
respectively.
It is clear that the electronic problem in the tight-binding model with a built-in symmetry-adapted scheme is a 2s x 2s matrix eigenvalue problem. The solutions of the matrix equation above are the eigenvalues Eklm and the eigenvectors cklm, m =1, 2, …, 2s. This equation has to be solved for all values of l, i.e., N times, and for as many values of k as needed.
Therefore, the problem for the unit cell of 2N atoms, which needs CPU time increasing
as N3, is reduced to a
linear-N problem by explicitly
accounting for the helical symmetry of the tubes.
The
symmetry-adapted tight-binding model presented above has won wide popularity in
the last few years because it allows for the accurate prediction of the optical
transition energies of any nanotube of practical interest. Recently, this model
has been adopted under the name extended
tight-binding model by Dresselhaus et al., who rederived the optical transition energies already published in
Refs. [1,2].
References
1. V. N. Popov, New J. Phys. 6 (2004) 1-17.
2. V. N. Popov and L. Henrard, Phys. Rev. B 70 (2004) 115407.
Valentin Popov
June 24, 2006