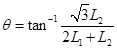Optimized structure of single-walled carbon nanotubes (SWNTs)

Fig. 1. Folding of a graphene sheet into a nanotube. A two-atom unit cell can be mapped unto the entire sheet by means of two primitive translations a1 and a2.

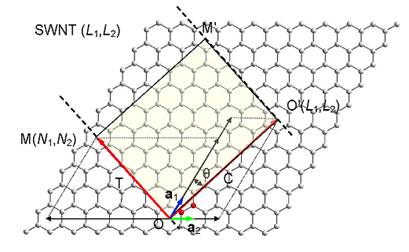
A nanotube can be obtained by cutting an infinite strip of a graphene sheet (Fig. 1) perpendicular to the chiral vector Ch = L1a1 + L2a2 = (L1,L2), through its beginning and end points, O and O', and folding the strip into a seamless cylinder. The nanotube is uniquely specified by the pair of integers (L1,L2). Alternatively, the nanotube can be specified by its radius R = Ch/2π and the chiral angle θ (the angle between the chiral vector and the nearest zigzag of carbon-carbon bonds). R and θ are given by the following relations , . The nanotube has a translational periodicity with primitive translation T = (N1,N2). The unit cell of the nanotube contains N carbon pairs. 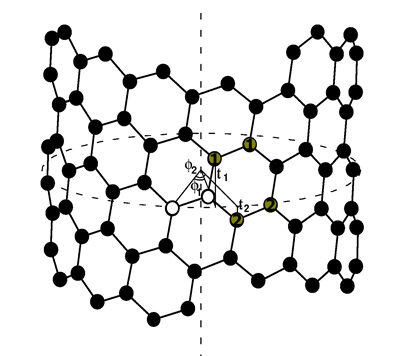N1, N2, T, and N are given by the relations , , , , where d is the greatest common divisor of 2L1 + L2 and L1 + 2L2. The nanotube has helical symmetry similar to the translational symmetry of graphene. Namely, graphene can be constructed by linear combinations of the two primitive translations of a given carbon pair. Similarly, a nanotube can be constructed by linear combinations of two screw operations executed on a carbon pair. A screw operation {S|t} consists of a rotation at an angle φ about the tube axis and a translation at a vector t along the same axis (Fig. 2). The parameters φ and t are given by , , , . There is an additional screw operation {S'|t'} coinciding one of the atoms of the carbon pair with the other, defined by the parameters φ' and t' , . The folded tube structure should be relaxed. Assuming conservation of the cylindrical geometry of the tube, the number of independent parameters can be as low as four. A suitable set of such parameters is the following one [1,2] . The relaxed values of these parameters, obtained within a non-orthogonal tight-binding model, are discussed in Refs. [1,2] and are available for download. References: 1. V. N. Popov, New J. Phys. 6 (2004) 1-17. 2. V. N. Popov and L. Henrard, Phys. Rev. B 70 (2004) 115407.

Fig. 2. Front view of a nanotube showing the two-atom unit cell (empty symbols). A two-atom unit cell can be mapped unto the entire tube by means of two different screw operations. A screw operation is defined by the rotation angle φ and the translation vector t. The one screw operation coincides the pair at the origin denoted by empty circles with the one labeled by"1". The other screw operation coincides the pair at the origin with the one labeled by "2". A third screw operation coincides one of the atoms of the pair with the other one.

Back

Valentin Popov

August 26, 2005